[TOC]

概述

电力系统线路稳态信号为50HZ的交流正弦（余弦）信号。对这个信号进行一个周期的一路信号进行采样，再进行离散傅立叶变换，可以得到这个时刻的频域信息。

其中，电力系统向量计算就是求出同一时刻所有线路的基波（ 50HZ频域分量）相位，进行快速的向量计算是提升电力系统测量控制系统性能的一大关键。

计算方法推导

离散傅立叶变换公式为：

$$X(k)=DFT[x(n)]=\sum_{n=0}^{N-1}x(n)W_N^{kn}$$

N为离散时间序列的点数，$W_N=e^{-j\frac{2\pi}{N}}$称为为旋转因子，是频率转换算子。进行离散傅立叶变换即可得出采样频率 N等分点的频域信息。

可看出其算法复杂度为($N^2$)，计算量非常大。而现实中人们采用快速傅立叶变换 FFT来进行计算的改进。改进思路就是从旋转变量的性质出发，进行乘法的缩减，形成迭代运算。
旋转变量的性质有：

$$
\begin{align}
W_N^{(k+N)n}&=W_N^{k(n+N)}=W_N^{kn}\newline
W_N^{k(N-n)}&=W_N^{-kn}=(W_N^kn)^*\newline
W_N^{k+\frac{N}{2}}&=-W_N^k
\end{align}
$$

其中基2FFT算法运用周期性(1)和半周期对称性(3)可将算法复杂度减小为($N\times log{2}N$),在这基础上再利用半周期共轭性质(2)的基4FFT算法可将算法复杂度减小为($\frac{N}{2}\times log{2}N$)。

向量计算中因为只需要50HZ处的频域信息，因此做FFT得到全部的N点频域信息会造成计算量的浪费。这里假设对线路采样为一个周期2000点，即采样频率为100Khz。经过一个周期的采样，对2000点等间隔选取128点进行FFT运算，得到一个相位信息。实际上50HZ的信息就是FFT运算后的第二点，向量合成只需要这一点的信息就可以。

基波相位信息即 k=1 的离散傅立叶变换：

$$X(1)=\sum_{n=0}^{N-1}x(n)W_N^n$$

其旋转因子为复平面单位圆上的以 (1,0)为起始点的N等分点：

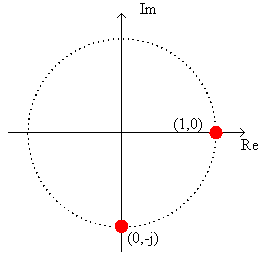
可以看出其运算复杂度变为(N)，已大大小于N点FFT。再利用半周期对称性(2)，可将运算复杂度降为(N/2)，相当于只用进行下半圆周的旋转因子乘法运算。再观察下半圆周的旋转因子分布，可看出前后1/4周期的旋转因子关于虚轴对称，即实部相反、虚部相等，这样就可以将运算复杂度降为(N/4)，再加上两个1/4周期的起始点(1,0)与(0,-j) 处是不用进行乘法运算的，这样计算效率又可以得到提升。

使用这一算法的另一个好处是，采样点的个数选取更为灵活，选取N=4M即可，不用选取N=2M或N=4M以配合基2FFT以及基4FFT 。

运用这种算法，再配合DSP芯片的高性能乘法运算以及内置的旋转变量数据表，可以获得高性能的向量计算效果。